در این آموزش قصد دارم تا شما را با تابع جبری مدارات منطقی و اصطلاح مینترم آشنا کنم. تابع جبری چیست و چرا باید از این روش استفاده کنیم؟ این سوال ممکن است برای خیلی از افراد مبتدی که تازه شروع به فعالیت در بحث مدارات منطقی کرده باشند، پیش بیاید. اما جواب این سوال چیست؟؟ بزارید با یک مسئله ساده این موضوع را برایتان توضیح بدم.
در ورزش فوتبال همیشه تیمی برنده میشود که تاکتیک و برنامهای از پیش آماده داشته باشد؛ خیلی وقتها تیم های خیلی کوچک با برنامهریزی و مدیریت درست جلوی تیم های بزرگ موفق ظاهر میشوند و حریف خود را شکست میدهند.
مدارات منطقی هم به همین صورت میباشند. یعنی قبل از اینکه یک مدار منطقی را بصورت عملی درآوریم ابتدا باید محاسبات و مدار تئوری آنرا به درستی بررسی و رسم کنیم. افراد مبتدی در پروژههای ساده ابتدا مدار عملی را میببندند و هنگامی که با نواقص و اشکالات مدار روبهرو میشوند، تصمیم میگیرند که مشکل را رفع کنند و به بررسی مدار بپردازند.
شاید اینکار در انجام پروژه های ساده و دانشجویی زیاد موضوع خاصی نباشد. اما هنگامی که قرار است یک پروژه صنعتی و حرفهای را طراحی کنیم بدلیل مخاطرات و هزینه بالا، این روش اشتباه است. روش درست این است، که ابتدا استراتژی و برنامهای مشخص شده را طراحی کنیم.
برای هر مدار منطقی و دیجیتال میتوانیم جدول صحت (Truth Table) و تابع جبری طراحی و ترسیم کرده و پس از بررسی اولیه مدار، سختافزار عملی آن را با توجه به تابع جبری و محاسبات از پیش انجام شده پیادهسازی و به اجرا درآوریم.
مینترم (minterm) توابع جبری
در یک مدار منطقی (تابع جبری مدار)، به تعداد متغیرهایی که در تابع وجود دارد (خود متغیرها یا معکوس not آنها)، به آن عبارت جبری مینترم میگوییم. به اطلاعات مربوط جدول مینترم، دیتا مینترم (Data Minterm) گفته میشود.
برای مثال یک گیت منطقی AND را در نظر بگیرید که دارای سه ورودی A،B،C میباشد و دارای یک خروجی Y است. مینترم حاصل از خروجی این تابع جبری به صورت زیر خواهد شود.
Y = ABC
مینترم تابع تعریف شده برابر ABC میباشد؛ زیرا تنها حالت برای اینکه 1 منطقی را در خروجی داشته باشیم این است که تمام ورودی ها برابر 1 منطقی باشد. به عبارت سادهتر میتوان گفت که مینترم به خروجی هایی از یک مدار منطقی گفته میشود که برابر 1 منطقی باشند.
| خروجی Y | ورودی سوم C | ورودی دوم B | ورودی اول A | شماره سطر جدول |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 1 | 1 | 0 | 3 |
| 0 | 0 | 0 | 1 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 0 | 1 | 1 | 6 |
| 1 | 1 | 1 | 1 | 7 |
همانطور که در جدول بالا مشخص است، تنها حالت برای اینکه خروجی برابر 1 منطقی شود؛ این است که تمام ورودی ها برابر 1 منطقی باشند؛ یعنی سطر شماره 7 جدول.
رابطه خروجی با توجه به شمارهی سطر به صورت زیر نوشته میشود:
Y = Σm (m7)
یا میتوان آن را به شکل زیر نشان داد:
(Y = Σm (7
Σ (سیگما) به معنای حاصل جمع یا همان مینترم است. معنی این معادله جبری یعنی خروجی تابعی که حاصل جمع سطرهای 7 است. اینجا تابع فقط یه خروجی دارد اما چنانچه خروجی دیگر حالتها برابر 1 منطقی باشد، باید دیگر حالتها را نیز اعمال و مدنظر گرفت.
مثال: جدول صحت و تابع خروجی Y = Σm (1,3,5,6) را بنویسید
1) درمرحله اول باید صورت مسئله و دادهها را ثبت و بررسی کرد. بر اساس فرض مسئله، خروجی تابع در سطرهای 1،3،5،6 برابر 1 منطقی است (خروجی بقیه سطرها برابر صفر منطقی خواهد بود).
2) جدول صحت تابع را رسم میکنیم (در این جدول بر اساس سیستم باینری به ازای شماره سطر باید مقادیر ستونی را مقداردهی کرد).
| خروجی Y | ورودی سوم C | ورودی دوم B | ورودی اول A | شماره سطر جدول |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 1 | 1 | 1 | 0 | 3 |
| 0 | 0 | 0 | 1 | 4 |
| 1 | 1 | 0 | 1 | 5 |
| 1 | 0 | 1 | 1 | 6 |
| 0 | 1 | 1 | 1 | 7 |
3) عبارت تابع خروجی را مینویسیم.
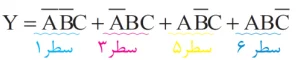
نکته: به خط بالای حروف، “NOT” گفته میشود. چنانچه این علامت بالای حرفی قرار بگیرد، به این معناست که مقدار ورودی آن حرف، برابر 0 منطقی است. برای مثال چون در سطر اول فقط ورودی C برابر 1 منطقی بوده، روی بقیه حروف علامت not قرار میدهیم.
به دست آوردن مینترم با استفاده از نرم افزار
خروجی توابع منطقی را میتوان به کمک نرم افزار به دست آورد. در ویندوز از نرم افزار مولتی سیم و در اندروید از نرم افزار Kamp Solution میتوان استفاده کرد.
ویندوز
نرم افزار مولتی سیم یکی از نرم افزارهایی است که قابلیت سادهسازی توابع جبری را دارد. این نرمافزار قابلیت برقراری ارتباط بین جدول صحت، تابع جبری و همچنین مدار عملی (سخت افزار) را فراهم میکند. با استفاده از این نرمافزار میتوانید مقادیر جدول صحت را مقداردهی کنید؛ سپس نرمافزار تابع و مدار مربوطه را برای شما رسم میکند (میتوانید به صورت معکوس نیز این کار را انجام دهید).
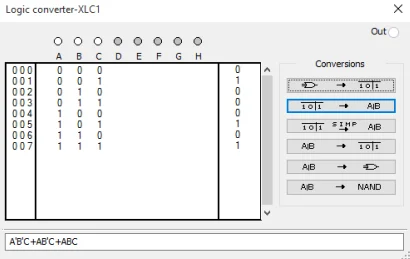
اندروید
برای ساده سازی توابع منطقی در سیستم عامل اندروید نرم افزار های زیادی وجود دارد؛ اما نرم افزار Kamp Solution توسط ما پیشنهاد میشود.
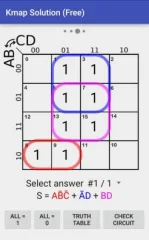
جمع بندی
کلام آخر اینکه همیشه قبل از حل هر مسئلهای باید ابتدا به راه حل فکر کنید و سپس روش حل موضوع را انتخاب کنید؛ این موضوع برای توابع جبری و مدارات منطقی نیز صدق میکند. شاید مسئلهای که در این پست حل کردیم ساده بود، اما تمامی مسائل به این سادگی نمیباشند و مسئله ذکر شده صرفا جنبه آموزشی داشت. امیدوارم که این مطالب براتون مفید بوده باشد. چنانچه سوال و ابهامی دارید میتوانید در قسمت دیدگاه، سوالتان را مطرح کنید تا در اسرع وقت به پاسخ برسید.


2 پاسخ
تابع سه متغیره ای طراحی کنیدبطوریکه اگرورودی 0,1,2,3باشد،خروجی یک واحدافزایش واگرورودی4,5,6,7باشد،خروجی یک واحدکاهش یابد؟ممنون میشم حلش کنین
کافیست یک تابع تعریف کنید و ورودی آن را 4 متغیر از نوع int با اسم دلخواه بزارید سپس در داخل تابع دو عدد if تعریف کنید که هر کدام مقادیر ورودی را ابتدا به صورت and مقایسه کرده سپس اگر شرط برقرار بود مقادیر را یک واحد کم یا زیاد کند.در انتها نام تابع را با ورودی ها در حلقه اصلی برنامه فراخوانی کنید. بهش فکر کنید بسیار ساده است …