آموزش ++C | بخش هفتم – توابع در c++

سلام دوستای خوبم. تا اینجای کار مفاهیم پایه زبان ++C رو براتون گفتیم. در این بخش از آموزش در مورد توابع در c++ و همچنین مفهموم چند ریختی توابع صحبت می کنیم. از اینجا به بعد مفاهیم یکم تخصصی تر و پیچیده تر میشه و نیاز به تمرین زیاد داره تا ملکه ذهن بشه. برای این که بتونید به صورت کامل از آموزش استفاده کنید، توصیه می‌کنم حتما قسمت‌های قبلی آموزش به خصوص بخش ششم آموزش c++ رو دنبال کنید. با ما در رزدینو همراه باشید.

تابع چیست؟

هرگاه در هر کجای برنامه بخواهیم از یک سری دستور که همه ی آن ها یک کار مشخص انجام می دهند، استفاده کنیم از توابع کمک می‌گیریم. توابع در c++ می توانند توسط خودمان نوشته شوند و یا اینکه بعضی از عملیات‌های ریاضی مثل گرفتن سینوس و کسینوس و … توسط توابع آماده انجام می شوند. فرم کلی تعریف یک تابع بصورت زیر است:


<پارامترهای ورودی) نام تابع <نوع برگشتی){
مجموعه دستور
}

<پارامترهای ورودی) نام تابع <نوع برگشتی){

مجموعه دستور

}

هر تابع از چهار قسمت تشکیل شده است. نوع برگشتی مقداری است که پس از برگشت از تابع بازگردانده می شود. نام تابع که شناسه اصلی تابع است و هرجای برنامه به این اسم شناخته می شود. پارامترهای ورودی برای مواقعی است که اجرای دستورات داخل تابع به پارامتری وابسته باشد. دستوراتی که قرار است این تابع انجام دهند درون بلاک {} نوشته می شوند.

توابع در c++

تابع غیر بازگشتی

تابعی است که پس از اتمام هیچ مقداری را برنمی گرداند. در این صورت نوع بازگشتی آن void تعریف می شود.


void print(){
cout << "Hello World!" << endl;
}

int main()
{
print();
getchar();
return 0;
}

void print(){

cout << "Hello World!" << endl;

}

int main()

{

print();

getchar();

return 0;

}

ساده ترین نوع تابع، تابعی است که نه مقدار ورودی دارد و نه مقداری را باز می گرداند. در مثال بالا یک تابع به نام print تعریف شد که کد داخل آن رشته !Hello World را چاپ می کند.

فرض کنید بخواهیم تابعی بنویسیم که دو عدد را گرفته و حاصل جمع آن دو را نشان دهد. به مثال زیر توجه کنید:


void sum(int a, int b){
cout << (a + b) << endl;
}

int main()
{
sum(2, 5);
getchar();
return 0;
}

void sum(int a, int b){

cout << (a + b) << endl;

}

int main()

{

sum(2, 5);

getchar();

return 0;

}

خب. تابعی به نام sum نوشتیم که دو متغیر به نام a و b از نوع int در ورودی دارد. پس موقع فراخوانی تابع باید دوعدد صحیح به آن بدهیم. در درون تابع حاصل جمع a + b بر روی کنسول چاپ می شود. نتیجه نهایی برنامه 7 است.

تابع بازگشتی

اگر بخواهیم پس از اجرای دستورات تابع، حاصل یا مقداری برگردانده شود، باید از کلمه کلیدی return استفاده کنیم. در این حالت باید نوع بازگشتی مشخص باشد و مقدار برگشتی هم، همان نوع باشد.


int sum(int a, int b){
int s;
s = a + b;
return s;
}

int main()
{
int x;
x = sum(2, 5);
cout << x << endl;
getchar();
return 0;
}

int sum(int a, int b){

int s;

s = a + b;

return s;

}

int main()

{

int x;

x = sum(2, 5);

cout << x << endl;

getchar();

return 0;

}

در کد فوق تابع sum دو عدد را گرفته، جمع کرده و حاصل را درون s می ریزد و سپس مقدار s را برمی گرداند. توجه شود که تعریف s درون تابع است و در بیرون از تابع نام s شناخته شده نیست. به این نوع متغیر، متغیر محلی گویند.

در درون تابع main یک متغیر محلی x تعریف شده که با صدا زده شدن تابع sum مقدار برگشتی این تابع درون x ریخته می شود. در نهایت مقدار x چاپ می شود. ذکر این نکته الزامیست که متغیر x محلی است و فقط داخل main قابل رویت می باشد.

توابع چند ریختی

هرگاه در برنامه خود دو تابع با نام های کاملا یکسان داشته باشیم اما نوع بازگشتی یا پارامترهای ورودی آن ها تفاوت داشته باشند، در این صورت آن دو تابع چند ریختی هستند. به مثال زیر دقت کنید:


void sum(int a, int b){
cout << (a + b) << endl;
}

void sum(int a, int b, int c){
cout << (a + b + c) << endl;
}

int main()
{
sum(2, 5);
sum(5, 9, 14);
getchar();
return 0;
}

void sum(int a, int b){

cout << (a + b) << endl;

}

void sum(int a, int b, int c){

cout << (a + b + c) << endl;

}

int main()

{

sum(2, 5);

sum(5, 9, 14);

getchar();

return 0;

}

در برنامه بالا دوتابع به نام sum داریم که اولی 2 پارمتر ورودی و دومی 3 پارامتر ورودی می گیرد. عملیات هر دو یکسان است و مقادیر ورودی را جمع می کنند و حاصل را نشان می دهند. اما نکته ای که حائز اهمیت است، در تابع main در خط 11 چون با صدا زدن تابع sum تنها دو ورودی به آن دادیم، پس کامپایلر بصورت خودکار تابع اولی را صدا می زند. همین قضیه برای خط 12 هم صادق است و بصورت خودکار تابع دومی انتخاب می شود. نتایج برنامه بصورت زیر است:


7
28

اگر نگاه کلی‌ای به توابع در c++ بیاندازیم، متوجه می‌شویم که توابع چند ریختی کابردهای بسیار زیادی در مباحث شی گرایی (که در آینده بیان می شوند) دارند و استفاده های آن بی شمار است.

توابع ریاضی

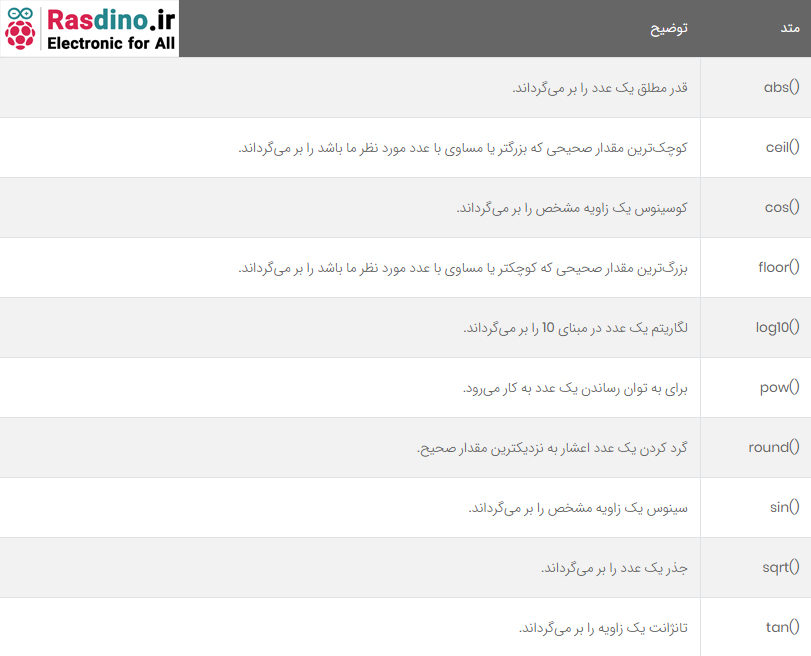
اگر بخواهیم در زبان ++C از عملیات ریاضی استفاده کنیم باید کتابخانه math.h را در اول برنامه include کنیم. توابع مهم ریاضی در جدول زیر بیان شده اند:

باید گفت که توابع مثلثاتی، زاویه ورودی آن ها بر حسب رادیان است و در صورت نیاز باید ابتدا درجه به رادیان تبدیل شود و سپس وارد تابع گردد. مثال:


#include <iostream>
#define _USE_MATH_DEFINES
#include <math.h>

using namespace std;
int main()
{
  int degree = 135;
  double rad = (M_PI / 180)*degree;
  cout << "sin(" << degree << ") = " << sin(rad) << endl;
  cout << "cos(" << degree << ") = " << cos(rad) << endl;
  cout << "tan(" << degree << ") = " << tan(rad) << endl;
  getchar();
  return 0;
}

#include <iostream>

#define _USE_MATH_DEFINES

#include <math.h>

using namespace std;

int main()

{

int degree = 135;

double rad = (M_PI / 180)*degree;

cout << "sin(" << degree << ") = " << sin(rad) << endl;

cout << "cos(" << degree << ") = " << cos(rad) << endl;

cout << "tan(" << degree << ") = " << tan(rad) << endl;

getchar();

return 0;

}

اول از همه توابع مورد نیاز iostream و math رو وارد کردیم. کتابخانه math یکسری ثابت هایی داره مثل عدد پی یا عدد e که برای استفاده از اونها باید قبل از وارد کردن math.h از دستور define _USE_MATH_DEFINES استفاده کنیم. این دستور به کتابخانه math میفهمونه که ما میخوام از ثابت ها استفاده کنیم و کتابخانه math اونها رو بصورت define برامون تعریف میکنه.

در تابع main یک متغیر نوع صحیح با مقدار اولیه 135 با نام degree داریم که مقدار آن به رادیان تبدیل شده و درون rad ریخته می شود. در نهایت هم نسبت های مثلثاتی 135 درجه چاپ می شود.


sin(135) = 0.707
cos(135) = -0.707
tan(135) = -1

sin(135) = 0.707

cos(135) = -0.707

tan(135) = -1

نکته: برای دسترسی به عدد پی از M_PI و دسترسی به عدد 2.7182 که به آن عدد exponential می گویند از M_E استفاده می کنیم.

توابع ریاضی غیر مثلثاتی

برای قدرمطلق گرفتن از تابع ()abs استفاده می شود.


double x = -5.3;
cout << abs(x) << endl;

double x = -5.3;

cout << abs(x) << endl;

5.3

5.3

اگر بخواهیم یک عدد را به سمت بالا گرد کنیم از تابع ()ceil استفاده می کنیم.


double x = 6.23;
cout << ceil(x) << endl;

double x = 6.23;

cout << ceil(x) << endl;

7

تابع ()floor برعکس تابع ()ceil است و به سمت پایین گرد می کند.


double x = 6.23;
cout << floor(x) << endl;

double x = 6.23;

cout << floor(x) << endl;

6

گرفتن لگاریتم در مبنای 10 توسط تابع ()log10 انجام می شود.


double x = 100;
cout << log10(x) << endl;

double x = 100;

cout << log10(x) << endl;

2

تابع ()pow برای به توان رساندن یک عدد به کار می رود. در مثال زیر مساحت یک دایره محاسبه می شود:


int main()
{
  double radius = 5.5;
  double masahat = M_PI * pow(radius, 2);
  cout << "Masahat = " << masahat << endl;
  getchar();
  return 0;
}

int main()

{

double radius = 5.5;

double masahat = M_PI * pow(radius, 2);

cout << "Masahat = " << masahat << endl;

getchar();

return 0;

}


95.030375

95.030375

رند کردن معمولی با تابع ()round انجام می شود. این تابع در صورتی که عدد وارد شده به آن بزرگتر یا مساوی 5. باشد به بالا رند می کند و اگر کوچکتر از 5. باشد به پایین رند می کند.


double x = 6.51;
cout << round(x) << endl;
double y = 6.49;
cout << round(y) << endl;

double x = 6.51;

cout << round(x) << endl;

double y = 6.49;

cout << round(y) << endl;

7
6

و در نهایت یکی از پرکابردترین توابع ریاضی تابع ()sqrt است که جذر یا ریشه دوم یک عدد را می گیرد.


double x = 16;
cout << sqrt(x) << endl;

double x = 16;

cout << sqrt(x) << endl;

4

این بخش از آموزش هم که مربوط به توابع در c++ بود، به اتمام رسید. در جلسه بعدی به مفاهیم مهم Call by value و Call by refrence پرداخته می شود.👋

بارزدینو همراه شوید در بخش بعدی آموزش ++C

محمد نصر

محمد نصر هستم. 9 سال سابقه کار در حوزه الکترونیک و همینطور برنامه‌نویسی میکروکنترلر به صورت پیشرفته دارم. سعی میکنم هر روز چیزهای جدید یاد بگیرم و خوشحال میشم با شما به اشتراک بگذارم.

4 پاسخ

شاهین گفت:

2021/10/31 در 21:14

سلام
آموزشتون از فرادرس کاملتره. دمتون گرم

پاسخ
1. محمد نصر گفت:
  
  2021/11/03 در 15:14
  
  ممنون از شما.
  
  پاسخ
کدرلایف گفت:

2023/04/20 در 07:13

ممنون از این مقاله کاربردی

پاسخ
ماشین بدون چرخ گفت:

2024/01/24 در 13:57

کاملترین و بهترین آموزش تو کل اینترنت واقعا فوق العاده بود مهندس جان فقط ی سوال من #define _USE_MATH_DEFINES را استفاده کرده قبل از کتابخانه اما با این حال M_PI شناسایی نشد. دلیلش چیه؟ بازم ممنون از آموزش های کاملتون هزاران گل تقدیم شما

پاسخ