درود بر مخاطبین رزدینو. در این پست قصد دارم شما را با سیستم اعداد آشنا کنم. بنظر شما کارکتر “F” چه معنی میتواند داشته باشد؟ این کاراکتر در مبنای سیستم شانزدهتایی/شانزدهی (Hexadecimal) در واقع همان عدد 15 در سیستم عددی دهدهی (Decimal) است!
شاید کمی گیج شده باشید و بگویید که سیستم عددی شانزده دهی یا دهدهی چیست؟ کاراکتر “F” چگونه معادل عدد 15 شده؟ اصلا سیستمهای عددی چی هستن و کجا کاربرد دارند؟ در این پست میخواهیم سیستمهای عددی را از صفر تا صد توضیح بدهیم. پس تا انتها، همراه ما باشید.
سیستم های عددی
سیستم عددی به سیستمی گفته میشود که دارای مجموعهای از اعداد، ارقام و گاهاً کاراکترها میباشد و هر کدام از آنها معنی خاصی دارند. بعضی وقتها این اعداد در زندگی روزمره ما به کار برده میشوند؛ اما بعضی اوقات این اعداد قابل فهم و درک ما نیستند و فقط کامپیوترها، تراشهها، آیسیها و … معنی این اعداد و ارقام را متوجه میشوند. سیستمهای عددی به منظور کاربرد خاص و مشخصی طراحی شدهاند.
برای مثال سادهترین سیستم عددی، سیستم عددی دهدهی میباشد که محدوده اعداد آن از عدد 0 تا 9 است و مجموعاً شامل ده عدد میشود و به همین منظور نامگذاری شده است. این سیستم در علم ریاضیات، کامپیوتر و … کاربرد وسیعی دارد. در زندگی روزمره هم از این سیستم برای “حساب و کتاب” روزانه در همهی امور استفاده خواهد شد.
معروف ترین سیستم عددی در علوم کامپیوتر، سیستم دودویی یا باینری است و مبنای اصلی زبانهای برنامه نویسی و کامپیوترها بر اساس این سیستم بوده و فقط شامل دو عدد 0 و 1 میباشد. شاید گاهاً کلی 0 و 1 در کنار هم ببینید و معنی آنها را متوجه نشوید؛ اما این بدین معنی نیست که این اعداد کاربردی ندارند.
توصیه: یکی از الزامات کار با انواع میکروکنترلرها نظیر AVR یا ARM، دانستن سیستم اعداد است.
سیستم های عددی پرکاربرد
در کل 4 سیستم عددی پرکاربرد داریم که عبارت اند از:
- سیستم دهدهی یا اعشاری (Decimal)
- سیستم دودویی یا دوتایی (Binary)
- سیستم هشتتایی یا اکتال (Octal)
- سیستم شانزدهتایی یا هگزادسیمال (Hexadecimal)
در ادامه به بررسی این سیستمهای عددی و نحوه تبدیل آنها به یکدیگر میپردازیم.
سیستم اعداد دهدهی یا اعشاری (Decimal)
این سیستم عددی پر کاربرد ترین سیستم عددی میباشد و به نام سیستم عددی روزمره نیز معروف است. در این سیستم ده رقم وجود دارد و به همین علت سیستم دهدهی نامیده میشود. این ده رقم شامل عدد 0 تا 9 است. در سیستم عددی دهدهی کوچکترین عدد 0 و بزرگترین عدد 9 است. به مثالهای زیر دقت کنید.
- 526310
- 884310
- 57810
برای نوشتن اعداد در مبنای سیستم دهدهی ابتدا عدد مد نظر را نوشته سپس عدد 10 را به صورت کوچک در کنارش مینویسیم.
نکته: برای نشان دادن سیستم عددی، عدد نوشته شده باید در قسمت پایین سمت راست عدد نوشته شود. توجه کنید که مبنای عددی باید بصورت رقم نوشته شود نه چیز دیگری.
سیستم عددی دودویی (Binary)
در سیستم عددی دودویی فقط دو عدد 0 و 1 وجود دارد. به همین دلیل به این سیستم، دودویی میگویند. برای نشان دادن اعداد بزرگتر از یک، ارقام 0 و 1 را با قواعد خاصی کنار یکدیگر قرار میدهند. برای مشخص کردن اعداد در این سیستم، عدد 2 را پایین سمت راست قرار میدهیم. به مثالهای زیر دقت کنید.
- 2(01001111)
- 2(111011111)
- 2(0000011001)
ساختار قرار گرفتن اعداد در سیستم باینری به صورت زیر است.
2(BN …. B4 B3 B2 B1)
بجای B، میتوان دو عدد 0 و 1 را قرار داد. اعداد کنار B، نشان دهنده تعداد ارقام است (توجه کنید ارزش مکانی نیست بلکه رقم شمارنده است).
به هر رقم یک بیت (Bit) گفته میشود. مثلا عدد 111 یک عدد سه بیتی است؛ یا عدد 11001 یک عدد پنج بیتی میباشد. هشت بیت معادل یک بایت (Byte) است. واحد بزرگتر از بایت معادل 1024 بایت است که به آن کیلو بایت (210) گفته میشود.
در تصویر زیر ارزش مکانی سیستم باینری مشخص شده است. بیت اول از سمت راست همان B0 بوده و کم ارزش ترین بیت میباشد که به آن LSB (Least Significant Bit) میگویند. به آخرین بیت که در سمت چپ است، B7 گفته و به اصطلاح به آن با ارزش ترین بیت یا MSB (Most Significant Bit) میگویند.
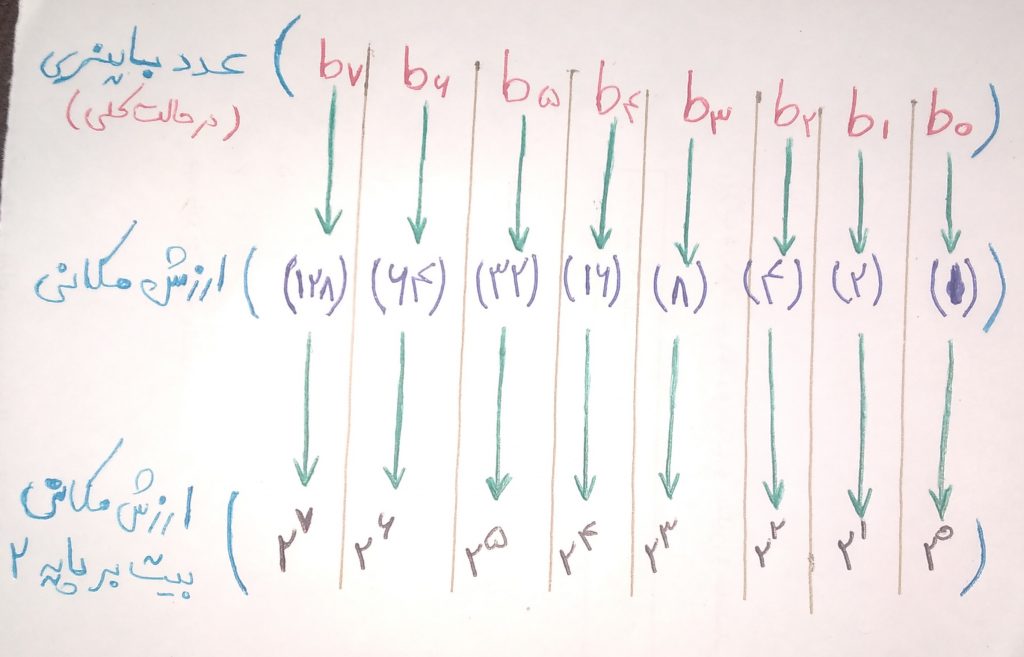
تبدیل اعداد باینری به دهدهی
برای تبدیل اعداد دودویی به دهدهی کافی است ارزش مکانی ارقام را با هم جمع کنیم. برای مثال میخواهیم عدد 1101 در مبنای باینری را به عدد دهدهی تبدیل کنیم.
1101 = (1 * 20) + (0 * 21) + (1 * 22) + (1 * 23) = 13 در مبنای دهدهی (اعشاری)
تبدیل اعداد دهدهی به باینری
برای تبدیل اعداد دهدهی به باینری از روش تقسیم متوالی استفاده میکنیم. به شکل زیر دقت کنید.
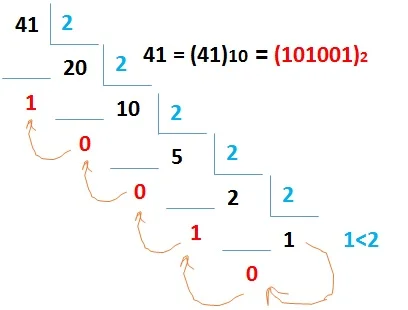
در این روش باید عدد مدنظر را بصورت متوالی بر عدد 2 تقسیم کنیم. این تقسیم تا جایی ادامه پیدا میکند که آخرین خارج قسمت برابر 1 باشد. سپس اعداد برحسب مراحل تقسیم در ارزش مکانی باینری جاگذاری میشوند. در جدول زیر اعداد 0 تا 15 در 4 مبنا آورده شدهاند.
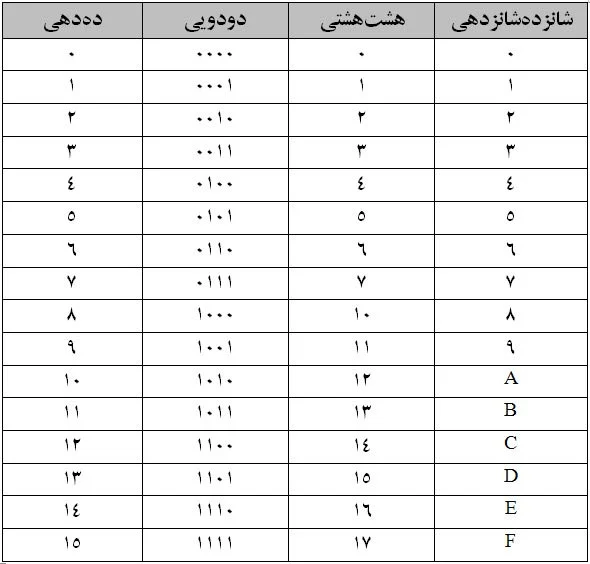
معمولا دانشجویان روش محاسبه تبدیل دهدهی به باینری و بلعکس رو یاد میگیرند؛ اما بعد از مدتی دوری از درس و امتحانات فرمولهای تبدیل را فراموش میکنند. معمولا طراحان و مخترعان که با مجموعهی محدودی از این اعداد سروکار دارند، سعی میکنند که این مجموعه اعداد را به حافظه خود بسپارند؛ اما گاها پیش میآید که محاسبه سنگین تر شده و باید محاسبه انجام داد. یکی از سادهترین روش ها برای تبدیل سیستمهای عددی، استفاده از ماشین حسابهای مهندسی است.
تبدیل سیستم اعداد به یکدیگر توسط ماشین حساب
سادهترین روش برای تبدیل اعداد استفاده از ماشین حساب ویندوز (Windows 10) است. برای اینکار مراحل زیر را دنبال کنید.
1- وارد ماشین حساب ویندوز (calculator) شوید.
2- روی سه خط بالا سمت چپ کلیک کرده و حالت محاسبه را روی Programmer قرار دهید.
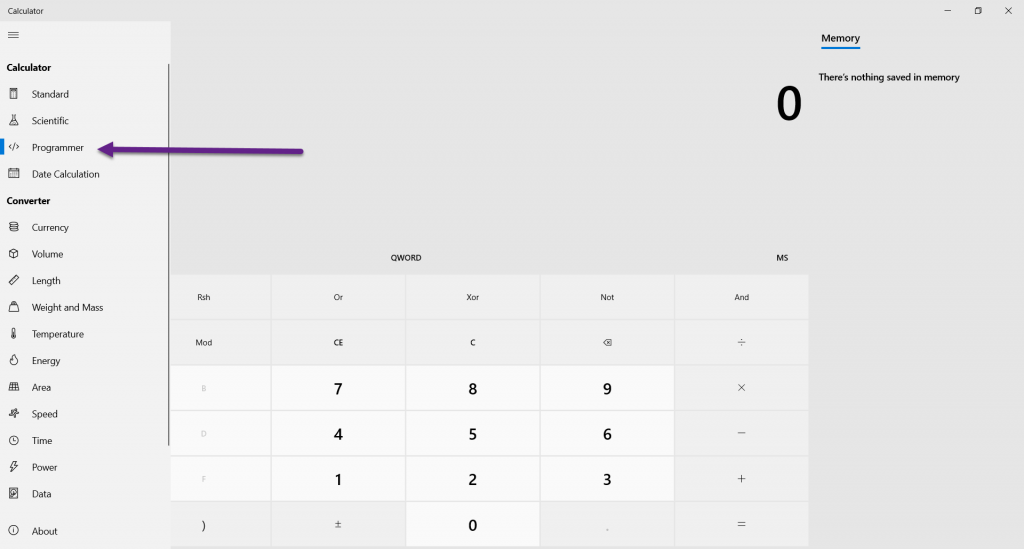
3- حال عدد مدنظر را وارد کرده و مقدار آن را در مبنایهای مختلف مشاهده کنید. در شکل زیر BIN مقدار دودویی، OCT مقدار هشت تایی، DEC مقدار دهدهی یا دسیمال و HEX مقدار شانزده تایی است.

سیستم اعداد هشت تایی یا اکتال (Octal)
در این سیستم مبنا عدد 8 بوده و از هشت عدد 0 تا 7 استفاده میکنیم. این سیستم عددی تقریبا منسوخ شده است و امروزه کاربرد کمتری نسبت به دیگر سیستم های عددی دارد؛ اما به عنوان یک مطلب برای یادگیری، مثال های زیر در مبنای 8 هستند و تبدیل آنها به دهدهی نیز آورده شده است.
- 568 = 46 در مبنای دهدهی
- 108 = 8 در مبنای دهدهی
- 1008 = 64 در مبنای دهدهی
- 3218 = (1 * 80) + (2 * 81) + (3 * 82) = 209 در مبنای دهدهی
تبدیل اعداد دهدهی به هشتتایی
برای تبدیل اعداد در سیستم دهدهی به سیستم هشتتایی باید عدد مدنظر(عدد دهدهی) در عدد 8 تقسیم متوالی شود. این فرآیند تا زمانی که آخرین خارج قسمت کوچکتر از 8 شود، ادامه پیدا میکند.
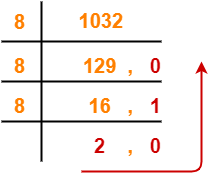
همانطور که در تصویر بالا ملاحضه میکنید، عدد 103210 را بصورت متوالی در عدد 8 تقسیم کرده و باقی مانده حاصل از تقسیم را به ترتیب از آخرین باقی مانده به اولین باقیمانده چینش میکنیم. بنابراین عدد فوق در مبنای 8 میشود 2010.
تبدیل اعداد هشتتایی به دهدهی
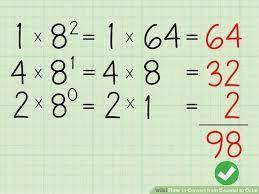
در مثال بالا عدد 1428 را به سه عدد 2 4 1 تقسیم کردیم؛ سپس به ترتیب در اعداد 80 و 81 و 82 ضرب کردیم و در نهایت حاصل همه موارد را با هم جمع کردیم. توجه شود که توان عدد 8 برگرفته شده از جدول ارزش مکانی است.
سیستم اعداد شانزده تایی یا هگزا دسیمال (Hexadecimal)
مبنای این سیستم عدد 16 میباشد؛ یعنی هر رقم میتواند یکی از اعداد 0 تا 9 و یا یکی از حروف A تا F باشد. ارزش هر رقم در جدول زیر مشخص است.
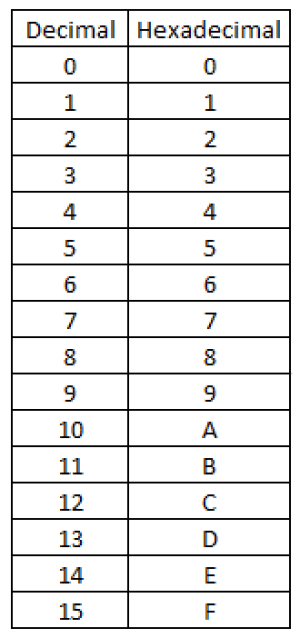
برای نشان دادن اعدادی که ارزش بیشتری از عدد 16دارند، اعداد و حروف مربوطه را طبق قواعد خاصی کنار یکدیگر قرار میدهیم.
تبدیل اعداد دهدهی به شانزدهتایی
برای تبدیل اعداد دهدهی به اعداد شانزدهتایی همانند روشهای قبلی، عدد مدنظر را باید بر عدد 16 تقسیم متوالی کنیم.
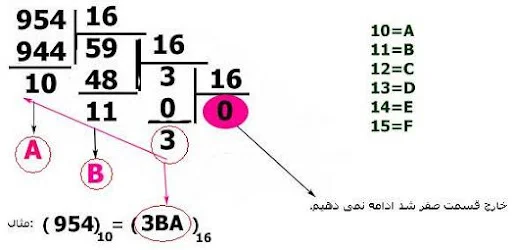
تبدیل اعداد شانزدهتایی به دهدهی

برای تبدیل سیستم شانزدهتایی به سیستم دهدهی همانند سیستمهای قبلی، طبق ارزشدهی موقعیت مکانی بیتها اعداد را از حالت شانزدهتایی به سیستم دهدهی تبدیل میکنیم. در مثال فوق عدد “A2F7” در مبنای شانزده است و ارقام آن به ترتیب در ضرایب 160، 161، 162 و 163 ضرب شده و با هم جمع شدهاند. حاصل نهایی 41719 در مبنای 10 است.
جمع بندی
در این پست به بررسی چهار سیستم عددی پرکاربرد پرداختیم. البته سیستمهای عددی دیگر هم وجود دارد اما مهمترین آنها این چهار سیستمی بود که در این پست آموزش داده شد. در علم مهندسی الکترونیک و مهندسی کامپیوتر در اکثر مواقع از دو سیستم دهدهی (اعشاری) و دودویی (باینری) استفاده میشود.
امیدواریم از محتوای این پست لذت کافی را برده باشید. چنانچه سوال، ابهام یا انتقادی نسبت به این پست دارید میتوانید در قسمت دیدگاه در انتهای این پست مطرح کنید.


8 پاسخ
ایول مهندس دست خوش
سلام ،،، عالی بود ،،، مرسی
خیلی ممنون عالی
عالی بود
دمت گرم خیلی خوب بود
عالییییییی مرسیییییی
خیلی عالی بود .دم شما گرم
عالی، خیلی ممنون از توضیحاتتون